📌 문제유형: DP
https://www.acmicpc.net/problem/1003
📌 풀이
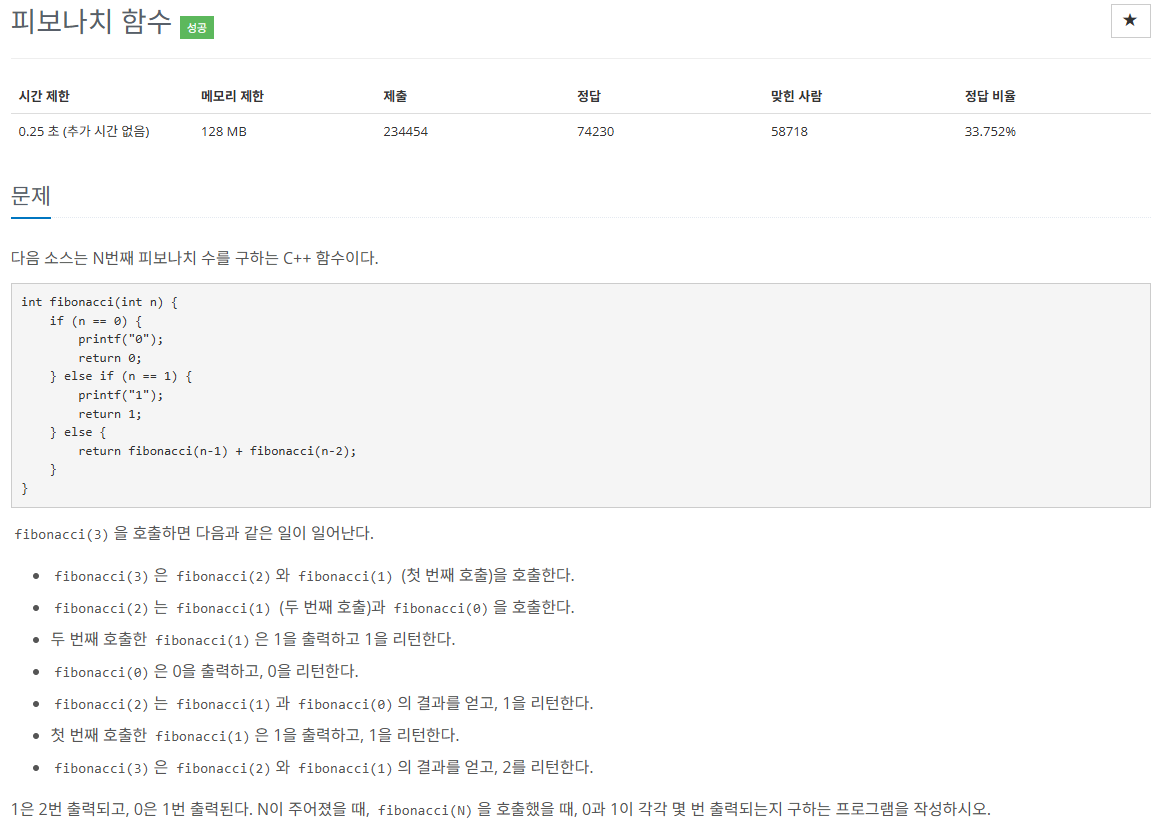
이 문제에서 포인트는 !!! 시간 제한이 0.25초 밖에 안된다는 점이다.
따라서 재귀함수로 작성하게 되면, 1시간초과에 걸리게 된다.
그 해결 방법은 동적 계획법(DP)에 있다.
즉, 메모제이션을 활용해야 한다.
메모제이션이란 앞서 계산했던 값을 저장해두어, 추후 다시 필요하게 될 때 다시 계산하는 것이 아니라 이미 계산된 값을 불러오는 것이다.
위의 문제는, n에 대한 피보나치 수열이 계산될 때 0과 1이 몇 번씩 필요로 되는가에 있다.
DP를 풀 때
1. 하나의 예제를 가지고 직접 손으로 적어보면서 실마리를 찾는다.
2. 규칙성을 찾아본다.
3. 이를 점화식으로 세워본다. (앞에서 #를 선택했을 때, #+1에서도 동일하게 작동되거나/ 뒤에서 #를 선택했을 때, #-1에서도 동일하게 적용되어 f(#-1), f(#)로 표현되곤 한다.)
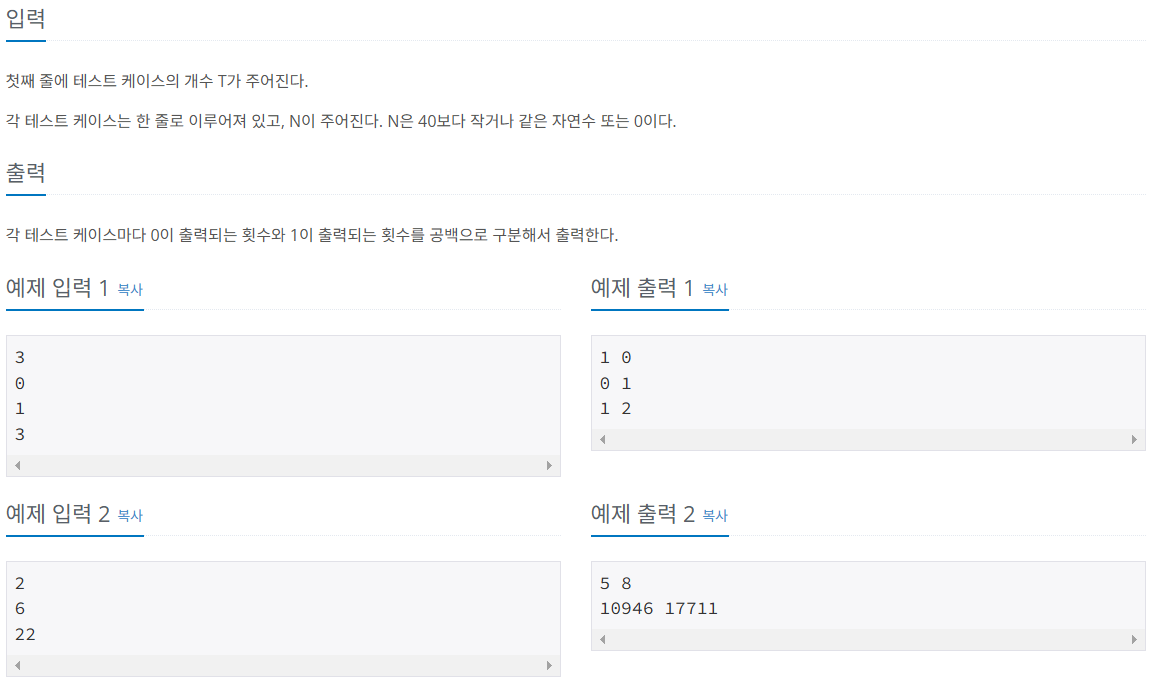
이 문제의 경우에는 아래와 같이 0과 1이 몇 번 호출되는지만 세어본다.
| 0 호출횟수 | 1 호출횟수 | |
| f(0) | 1 | 0 |
| f(1) | 0 | 1 |
| f(2) | 1 | 1 |
| f(3) | 1 | 2 |
| f(4) | 2 | 3 |
| f(5) | 3 | 5 |
| ... |
위처럼 된다고 했을 때, 규칙성을 찾아보자.
0의 호출횟수 먼저 보면, f(2) = f(1) + f(0)/ f(4) = f(3) + f(2)/ f(5) = f(4) + f(3) ...
즉, i가 0을 호출하는 횟수 = (i-1이 0을 호출하는 횟수) + (i-2가 0을 호출하는 횟수) 이렇게 정리가 된다.
1의 호출횟수 규칙도 0과 동일하다.
따라서, 이 점화식을 코드로 나타내면 아래와 같이 된다.
이때, zero_cnt와 one_cnt는 미리 초기화가 되어 있다. 41만큼 생성된 이유는, N이 40보다 작거나 같은 수이기 때문이다.
T = int(input())
# dp = [-1] * 41 ==> 굳이 필요없는 코드
# dp[0] = 0
# dp[1] = 1
zero_cnt = [0] * 41
one_cnt = [0] * 41
zero_cnt[0] = 1
one_cnt[1] = 1
for tc in range(T):
n = int(input())
if n > 1:
for i in range(2, n+1):
# dp[i] = dp[i-2] + dp[i-1]
zero_cnt[i] = zero_cnt[i-1] + zero_cnt[i-2]
one_cnt[i] = one_cnt[i-1] + one_cnt[i-2]
# 아래서부터 전부 계산해 올라가기
print(zero_cnt[n], one_cnt[n])
'코딩테스트 > BAEKJOON' 카테고리의 다른 글
| [백준/Python] 14940. 쉬운 최단거리 (1) | 2024.11.19 |
|---|---|
| [백준/Python] 1463. 1로 만들기 (1) | 2024.11.18 |
| [백준/Python] 17219. 비밀번호 찾기 (2) | 2024.11.18 |
| [백준/Python] 11047. 동전 0 (0) | 2024.11.18 |
| [백준/Python] 11399. ATM (0) | 2024.11.18 |