# [C언어로 쉽게 풀어쓴 자료구조(천인국)]를 공부하고 주요 내용을 정리하고자 작성하는 글입니다.
# 해당 게시글에 대한 모든 피드백 환영합니다.
위상 정렬 Topological Sort
각 정점들의 선행순서를 위반하지 않으면서 모든 정점을 나열하는 것
생각의 순서
1. 진입차수가 0인 정점을 선택한다. (정점이 여러 개인 경우, 임의로 하나를 고른다.)
2. 선택된 정점과 이 정점에 부착된 간선들을 모두 삭제한다.
3. 2번에서 선택된 정점과 인접했던 정점들의 진입차수를 -1 한다.
4. 모든 정점이 사라질 때까지 1~3 과정을 반복한다.
알고리즘
1 2 3 4 5 6 7 | topo_sort(G) if (모든 정점의 진입차수가 1 이상이면) then 위상정렬 불가 while 정점이 존재할때 do 진입차수가 0인 정점 v를 선택 v 를 출력 v와 v에서 나온 모든 간선들을 그래프에서 삭제 // v의 인접정점의 진입차수 -1 | cs |
그림으로 이해하기
아래의 방향 그래프에 대해 위상정렬을 수행해보자.
단, 핵심 키워드가 진입차수라는 점을 유의한다.

1. 정점 1과 1에 부착된 모든 간선들을 삭제한다.
==> 1의 인접정점들의 진입차수를 모두 -1한다.

2. 정점 0과 0에 부착된 모든 간선들을 삭제한다.
==> 0의 인접정점들의 진입차수를 모두 -1한다.

3. 정점 2와 2에 부착된 모든 간선들을 삭제한다.
==> 2의 인접정점들의 진입차수를 모두 -1한다.

4. 정점 3과 3에 부착된 모든 간선들을 삭제한다.
==> 3의 인접정점들의 진입차수를 모두 -1한다.
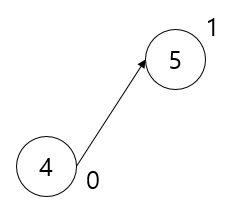
5. 정점 4과 4에 부착된 모든 간선들을 삭제한다.
==> 4의 인접정점들의 진입차수를 모두 -1한다.

6. 정점 5와 5에 부착된 모든 간선들을 삭제한다.
==> 5의 인접정점들의 진입차수를 모두 -1한다.
7. 그래프 내 모든 정점들이 삭제되었으므로 종료한다.
c언어로 구현
위상정렬을 구현하기 위해서는 스택stack과 연결리스트로 표현된 그래프를 이용한다.
- 우선, 그래프에서 진입차수가 0인 정점들을 모두 push한다.
- 스택에서 pop하여 정점을 하나 가져온다.
- 그 정점의 연결리스트에 가서 모든 인접정점의 진입차수를 1씩 뺄셈 연산을 수행한다. 뺄셈 연산을 수행한 직후에 진입차수가 0이 되는 정점은 바로 스택에 push한다.
- 이 과정을 스택이 공백상태가 될 때까지 진행한다.
앞서 예시로 들었던 방향그래프에 대해, 스택을 이용해 풀면 다음과 같다.

이를 한번 코드로 구현해보자.
#include <stdio.h>
#include <stdlib.h>
/****************************** graph **********************************/
#define MAX_VERTICE 50
// 각 정점마다 하나의 연결리스트가 필요하다
// 정점의 개수만큼의 포인터 배열(헤더노드)이 필요하다
// 하나의 노드 ==> GraphNode
// 포인터 배열의 이름 ==> adj_list
typedef struct GraphNode {
int vertex; // 정점의 값을 저장할 곳
struct GraphNode* link; // 인접정점을 가리킬 포인터
// 가리킬 변수의 타입이 하나의 정점이기 때문에 GraphNode 타입으로 선언해야 한다.
} GraphNode;
typedef struct GraphType {
int n; // 해당 그래프의 정점의 개수
GraphNode* adj_list[MAX_VERTICE]; // 정점들을 관리할 리스트; 헤더노드 집합
} GraphType;
// 그래프 초기화
void graph_init(GraphType* g) {
int v;
g->n = 0; //그래프 정점의 개수 0으로 초기화
for (v = 0; v < MAX_VERTICE; v++) {
g->adj_list[v] = NULL;
}
}
// 정점 삽입 연산: 값이 v인 정점을 삽입한다.
void insert_vertex(GraphType* g, int v) { // v: 삽입합 노드의 값
if ((g->n) + 1 > MAX_VERTICE) {
fprintf(stderr, "그래프: 정점의 개수 초과\n");
return;
}
g->n++;
}
// 간선 삽입 연산: 정점 u와 v를 연결한다 : 정점 u에 간선 (u,v)를 맨 처음에 삽입
void insert_edge(GraphType* g, int u, int v) {
if (u >= g->n || v >= g->n) {
fprintf(stderr, "그래프: 정점 번호 오류\n");
return;
}
GraphNode* node = (GraphNode*)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node; // adj_list의 한 원소는 GraphNode를 가리키는 포인터 타입이니까 할당 가능
}
/********************************** stack ***************************************/
#define MAX_STACK_SIZE 10
typedef int element;
typedef struct {
element stack[MAX_STACK_SIZE];
int top;
} StackType;
void init(StackType* s)
{
s->top = -1;
}
int is_empty(StackType* s)
{
return (s->top == -1);
}
int is_full(StackType* s)
{
return (s->top == (MAX_STACK_SIZE - 1));
}
void push(StackType* s, element item)
{
if (is_full(s)) {
fprintf(stderr, "Stack is Full\n");
return;
}
else
s->stack[++(s->top)] = item;
}
int pop(StackType* s)
{
if (is_empty(s)) {
fprintf(stderr, "Stack is Empty\n");
return;
}
else
{
return s->stack[(s->top)--];
}
}
void topo_sort(GraphType* g)
{
int i;
StackType s;
GraphNode* node;
int* in_degree = (int*)malloc(g->n * sizeof(int));
for (i = 0; i < g->n; i++)
in_degree[i] = 0;
for (i = 0; i < g->n; i++) {
GraphNode* node = g->adj_list[i];
while(node != NULL) {
in_degree[node->vertex]++; // 정점 i가 가리키고 있는 노드의 진입차수 1 증가
node = node->link;
}
}
init(&s);
for (i = 0; i < g->n; i++) {
if (in_degree[i] == 0)
push(&s, i);
}
int w;
while (!is_empty(&s))
{
w = pop(&s);
printf("정점 %d -> ", w);
node = g->adj_list[w];
while (node != NULL) {
int u = node->vertex;
in_degree[u]--;
if (in_degree[u] == 0) push(&s, u);
node = node->link;
}
}
free(in_degree);
printf("\n");
}
int main()
{
GraphType g;
graph_init(&g);
insert_vertex(&g, 0);
insert_vertex(&g, 1);
insert_vertex(&g, 2);
insert_vertex(&g, 3);
insert_vertex(&g, 4);
insert_vertex(&g, 5);
insert_edge(&g, 0, 2);
insert_edge(&g, 0, 3);
insert_edge(&g, 1, 3);
insert_edge(&g, 1, 4);
insert_edge(&g, 2, 3);
insert_edge(&g, 2, 5);
insert_edge(&g, 3, 5);
insert_edge(&g, 4, 5);
topo_sort(&g);
return 0;
}결과

'자료구조' 카테고리의 다른 글
| 트리 - 이진트리 정의/ 성질/ 분류/ 표현법 (0) | 2022.02.02 |
|---|---|
| 트리 - 개념/ 용어정리 (0) | 2022.02.01 |
| 그래프 - Floyd 알고리즘 (0) | 2022.01.31 |
| 그래프 - Dijkstra 알고리즘 (0) | 2022.01.31 |
| 그래프 - 최단경로 (0) | 2022.01.31 |